Regra de três simples é um processo prático para resolver problemas que
envolvam quatro valores dos quais conhecemos três deles. Devemos, portanto,
determinar um valor a partir dos três já conhecidos.
Passos par resolver a regra de três simples
1º) Construir uma
tabela, agrupando as grandezas da mesma espécie em colunas e mantendo na mesma
linha as grandezas de espécies diferentes em correspondência;
2º) Identificar se
as grandezas são diretamente (quando as duas crescem ou diminuem juntas) ou
inversamente (quando uma grandeza cresce e a outra diminui) proporcionais;
3º) Montar a
proporção e resolver a equação.
Exemplos
Com uma área de absorção de raios solares de 1,2m2, uma
lancha com motor movido a energia solar consegue produzir 400 watts por hora de
energia. Aumentando-se essa área para 1,5m2, qual será a energia
produzida?
Solução: montando a tabela:
|
Área (m2)
|
Energia
(Wh)
|
|
1,2
|
400
|
|
1,5
|
x
|
Identificação do tipo de relação:
:
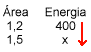
Inicialmente colocamos uma seta para baixo na coluna que contém o x (2ª
coluna). Observe que, aumentando a área de absorção, a energia
solar aumenta. Como as palavras correspondem (aumentando -
aumenta), podemos afirmar que as grandezas são diretamente
proporcionais.
Assim sendo, colocamos outra seta no
mesmo sentido (para baixo) na 1ª coluna.
Montando a proporção e resolvendo a equação temos:
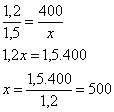 |
|
|
|
Logo, a energia produzida será de 500 watts por hora.
Um trem, deslocando-se a uma velocidade média de 400Km/h, faz um determinado
percurso em 3 horas. Em quanto tempo faria esse mesmo percurso, se a velocidade
utilizada fosse de 480km/h?
Solução: montando a tabela:
|
Velocidade
(Km/h)
|
Tempo
(h)
|
|
400
|
3
|
|
480
|
x
|
Identificação do tipo de relação:
Inicialmente colocamos uma seta para baixo na coluna que contém o x (2ª
coluna). Observe que, aumentando a velocidade, o tempo do
percurso diminui. Como as palavras são contrárias (aumentando -
diminui), podemos afirmar que as grandezas são inversamente
proporcionais.
Assim, colocamos outra seta no
sentido contrário (para cima) na 1ª coluna.
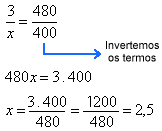
Montando a proporção e resolvendo a equação temos:
|
|
|
Logo, o tempo desse percurso seria de 2,5 horas ou 2 horas e 30
minutos.

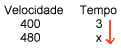
Nenhum comentário:
Postar um comentário