FUNÇÃO HORÁRIA DO ESPAÇO - MOVIMENTO UNIFORMEMENTE VARIADO (MUV)

Quando o intervalo de tempo for infinitamente pequeno, ou seja, 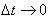, tem-se a aceleração instantânea do móvel.

Isolando-se o :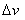

Mas, sabemos que:

Então:

Entretanto, se considerarmos , teremos a função horária da velocidade do Movimento Uniformemente Variado, que descreve a velocidade em função do tempo [v=f(t)]:

Posição em função do tempo

A melhor forma de demonstrar esta função é através do diagrama velocidade versus tempo (v x t) no movimento uniformemente variado.

O deslocamento será dado pela área sob a reta da velocidade, ou seja, a área do trapézio.

Onde sabemos que:

logo:

ou

Interpretando esta função, podemos dizer que seu gráfico será uma parábola, pois é resultado de uma função do segundo grau.