Radiciação é a forma de conhecermos a raiz de um determinado número. Sendo um tipo de representação de expoentes fracionários. Para entender radiciação é necessário entender também potenciação, que é ao inverso da radiciação.
Seja a um número real não negativo e n um número natural, com n ≥ 1, chamamos de raiz enésima de a se, e somente se, o número real x, não negativo, elevado ao expoente n, resulta em a, tal que xn = a.
Para representarmos radicais utilizamos o símbolo √, chamado de radical.
Dessa forma,
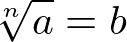
Onde n é o índice da raiz, a é o radicando e b a raiz. Leia-se: raiz enésima de a é igual a b.
Exemplo:
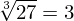
(Leia-se: raiz cúbica de 27 é igual a 3)
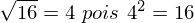
(Leia-se: raiz quadrada de 16 é igual a 4), quando não aparece o índice consideramos esse índice igual a 2.
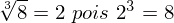
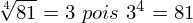
(Leia-se: raiz quarta de 81 é igual a 3)
A raiz quadrada de um número a é b, quando o elevamos b ao expoente 2, encontramos a. Veja o exemplo abaixo.
Exemplo:
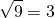
Leia-se: raiz quadrada de 9 é igual a 3. Neste caso, a raiz quadrada de 9 é 3, pois quando elevamos 3 ao expoente 2 encontramos o número 9.
Observação: quando não aparece o índice na raiz temos que esse índice é o número 2.
Da mesma forma que a raiz quadrada, a raiz cúbica de um número a é b, quando elevamos b a um expoente 3, temos a. Isso pode ficar mais claro com um exemplo. Veja!
Exemplo:
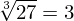
Nesse caso, a raiz cúbica de 27 é 3, pois 3 elevado ao expoente 3 é o próprio número 27.
Observações
Pela definição ocorre que
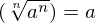
para qualquer a ≥ 0.
Também pela definição é possível observar que:
| Correto | Incorreto |
|---|---|
 |  |
 |  |
 |  |
 |  |
Cálculo da raiz quadrada de um quadrado perfeito:
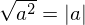
Exemplos:
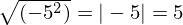
e não
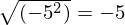
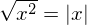
e não
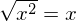
Considerando o conjunto dos números reais, caso n seja par ou ímpar temos situações distintas.
Considerando n par:
Para a < 0, não existe raiz enésima de a.
Exemplo: não existe raiz real para
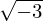
Para a = 0, a raiz enésima é zero.
Exemplo:
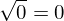
Para a > 0, temos somente um única raiz para a, que é:
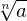
Considerando n ímpar:
Independente do número real a, existe somente uma única raiz enésima, indicada por:
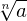
Exemplos:
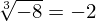
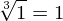
Propriedades da radiciação
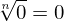
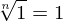
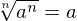
Nesse último caso podemos simplificar quando o índice é igual ao expoente, eliminando-o (“cortando”).
Propriedades operatória da radiciação
Seja a e b pertencente ao conjuntos dos números reais positivos, m pertencente ao conjuntos dos números inteiros e n e p pertencente ao conjunto dos naturais maiores que zero, temos as seguintes propriedades:
Radical de um produto
Quando temos no radicando uma multiplicação, podemos separar em radicais diferentes com mesmo índice.
Exemplo:
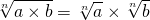
Radical de uma divisão
Quando temos uma divisão no radicando, podemos ter uma divisão de radicais.
Exemplo:
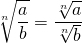
com b diferente de zero.
Mudança de índice
Se quisermos mudar o índice de um radical, podemos dividir o índice e o expoente do radicando por um número natural maior que zero.
Exemplo:
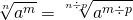
Radical de uma potência
Quando temos uma raiz elevada a um expoente, podemos atribuir esse expoente ao radicando.
Exemplo:
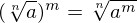
Simplificação de radicais
Quando temos uma raiz dentro da outra podemos simplificá-la colocando o radicando em uma só raiz e multiplicando os índices.
Exemplo:
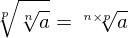

Nenhum comentário:
Postar um comentário